渐变折射率光纤
Problem
近期在阅读本书Chapter3的时候,遇到一个似曾相识的老问题,关于渐变折射率(Graded-index)光纤的纤芯折射率表达式。我第一次见到这个表达式是在本科三年级,学习光纤通信的时候,当时也觉得奇怪,为什么把这样的折射率分布称为“抛物型”,因为显然这并不是一个二次表达式(红框内部分)。

再次看见这个表达式,我不禁思考这玩意是怎么得到的。渐变折射率光纤只提到了渐变二字,理应只要满足折射率连续变化即可,为什么在各类教材中表达式都是这样的形式呢?
Self-focusing
查阅了不少光纤通信的教材,都没有提到这个表达式的由来,以我的思考,它应该是为了达成某种目的得到的最优解,所以才会被广泛采用。提到渐变折射率光纤,它最大的特性就是能够减弱色散,书本48页对比了多模下阶跃折射率和渐变折射率的理论最大比特率,分别是*10Mbit/s·km*和*8Gbit/s·km*,模间色散差别带来了接近一千倍的比特率之差。
之所以渐变折射率能够减弱模间色散,其中涉及到一个非常简单的原理,光速在折射率大的材料中较慢,也就是$v=\frac{c}{n}$ ,渐变型光纤的边缘折射率较低,高阶模在远离光纤轴心的位置传播时拥有更快的光速,也就弥补了其传播距离较长带来的额外光程。既然这样,通过合理设计光纤的折射率分布,能否实现高低阶模式传播光程相同呢,这样色散也就得以消除了。
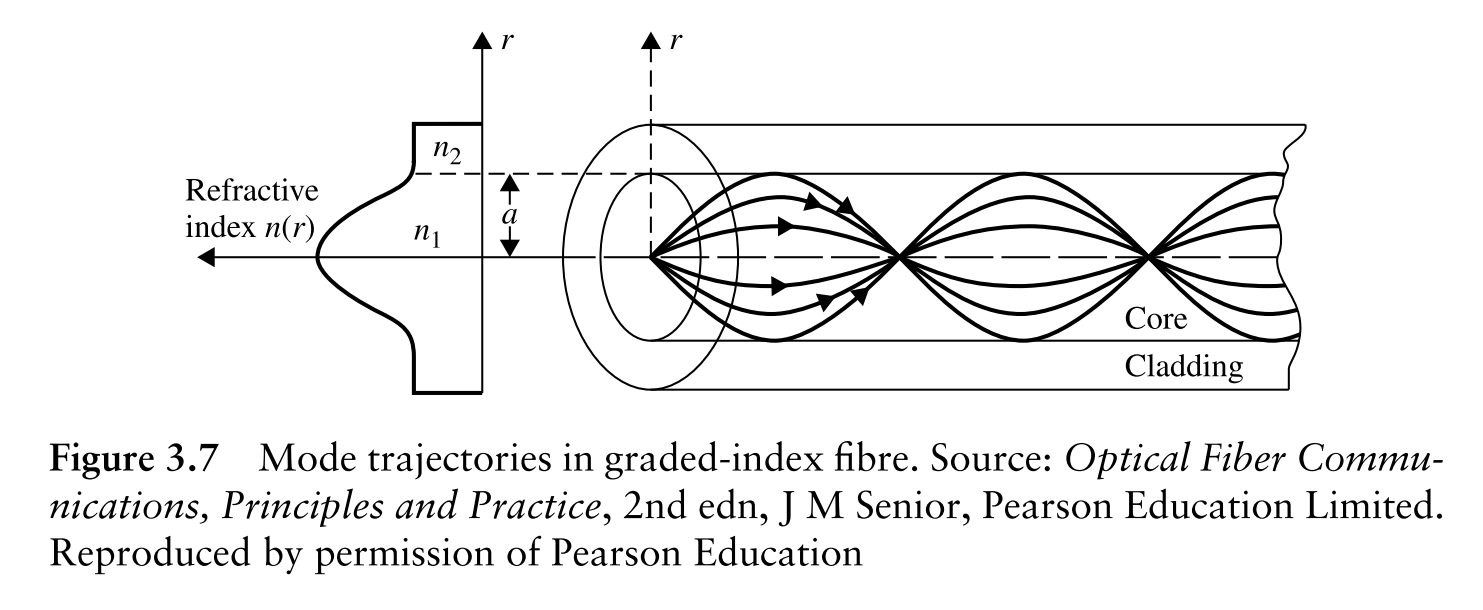
Figure3.7展示了一个典型的渐变型光纤内部不同模式传播的光路,注意不同模式的光总是随着传播距离,周期性地会聚又发散。而我们知道,根据费马原理(Fermat’s principle),过空间两定点的光路总是光程最短,可知上图中每一个光路交点之间的所有光线是等光程的。换句话说,如果不同模式的光到最后依然会聚在一个点上,那么色散也就不存在了。
我找到了式3.1a中$\alpha=2$时光纤满足自聚焦条件简短证明过程[1],以同样的方法逆推既应该可以得到前文中的折射率分布表达式。也就是说,在书中给出的表达式下,近轴不同模式的光线围绕光纤轴心呈周期性正弦摆动(强调近轴是因为实际上还是会有色散存在)。
以这种思路来看,式3.1a其实是满足自聚焦条件的一个渐变折射率表达式,能够实现较低的色散,满足通信传输的需求。
Wave Optics Analysis
众所周知,在分析波导光学的时候,除了直观的几何光学方法之外,常常采用更为精确的波动光学方法,也即电磁学方法。这里有几张我本科集成光学的PPT。


式3.1a中列出的折射率分布实际上是平方率分布,也就是能够通过电磁场分析得到精确解的分布形式之一。从这里,我们也可以看出,选中这样的一个表达形式绝对是深思熟虑的结果。
至于具体的缘由,到目前为止,我还没有得出一个确切的结论。受制于我的知识储备水平和数理分析能力,我还没有很好地解决当前的疑问,但也确实收获了不少相关知识。即便光纤通信可能与我的具体方向牵扯不深,我认为追究到底是有必要的。
此后若有新的理解,我会予以更新。
Matlab Simulation
书中有这样的一幅图,其实就是折射率分布的直观体现。
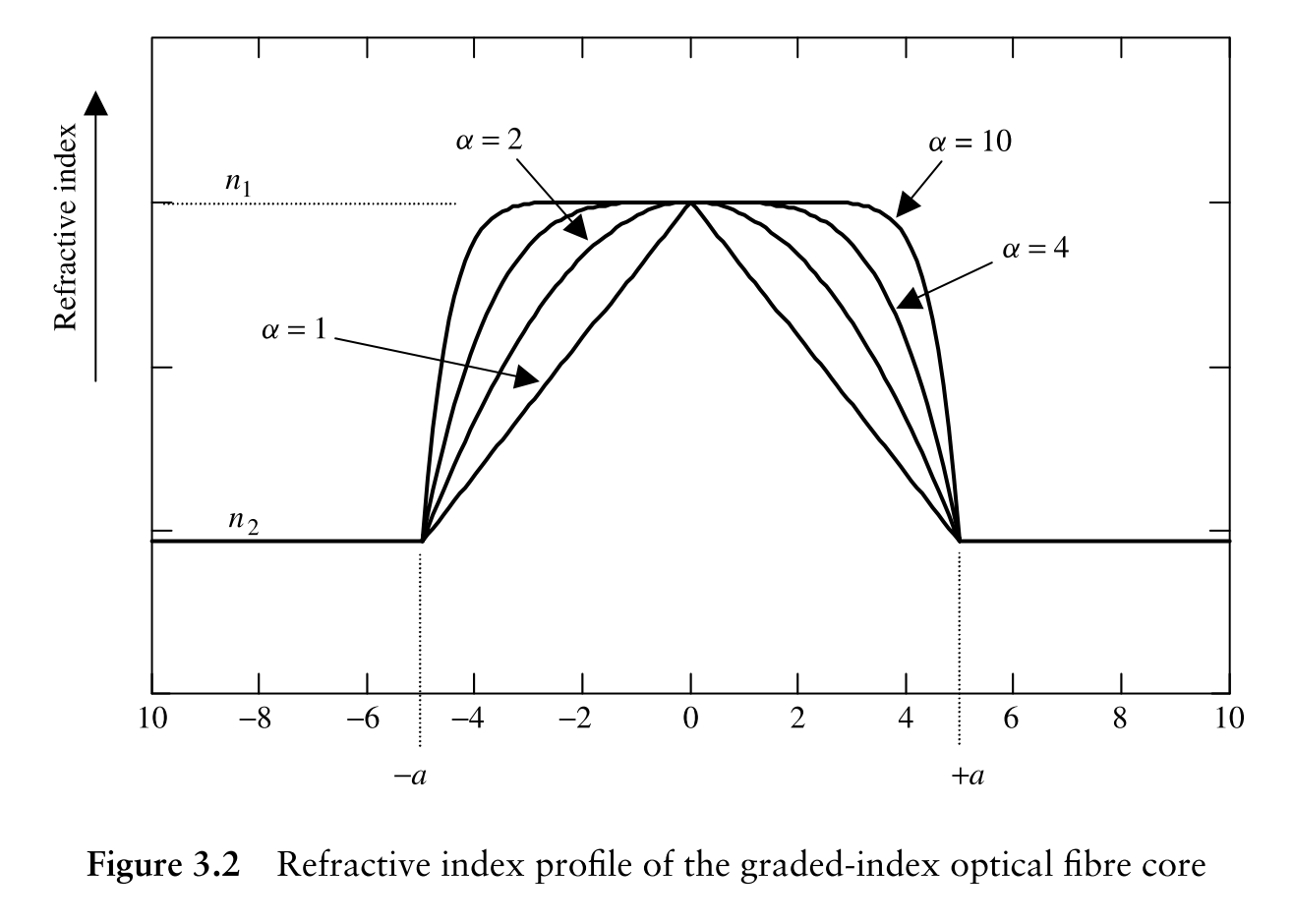
这里$\alpha=1$的曲线是一个折线,而且在平方率折射率分布中被称为“三角分布”。直观来看,这确实是一个三角,在表达式中却很难看出它竟是线性的。因此我绘制了对照图形,虚线为真实的线性分布,可以看出和$\alpha=1$的状态还是有所差别,从图二中可以观察得更为明显。


使用的脚本如下:
a=5;n1=1.3;n2=1.1;
r=linspace(-5,5,1000);
lr=n1-r*(n1-n2)/a;
lr_=fliplr(lr);
lrr=[lr_(1,1:500),lr(1,501:1000)];
plot(r,lrr,'--k'),hold on
plot([-2*a,-a],[n2,n2],[a,2*a],[n2,n2])
nl=[1,2,4,10];
for i=1:4
d=(n1^2-n2^2)/(2*n1^2);
n=n1*sqrt(1-2*d*(r./a).^nl(1,i));
n_=fliplr(n);
nn=[n_(1,1:500),n(1,501:1000)];
plot(r,nn)
end
title('graded-index variation')
ylim([1,1.4])
legend('linear','\alpha=1','\alpha=2','\alpha=4','\alpha=10')
figure
plot(r(501:1000),lrr(501:1000),'--k'),hold on
plot(r(501:1000),n1*sqrt(1-2*d*(r(501:1000)./a)))
legend('linear','\alpha=1')
title('linear & \alpha=1')参考文献:
[1] 张晓光. 自聚焦多模光纤模式色散的几何光学与波动光学处理方法[J]. 物理与工程, 2017, 27(1): 23-29, 43.
2019.7.24 @ZY